Subtitle: From a new formalization of normative theory building
This is a crosspost from my blog, Irrational Community. If you enjoyed this, please check it out!
Note: I will only be presenting a very brief overview of the arguments for and against fanaticism. For more detailed academic treatments, see for and against; for more accessible, layperson-friendly discussions, see for and a for and against.
Also, this post has a lot of optional footnotes. Some are just clarifications, others go deeper into the weeds. Feel free to ignore them if you’re following along. [1]
Fanaticism in decision theory and moral philosophy refers to the idea that outcomes with extremely large (often infinite or astronomically high) payoffs dominate decision-making, even if their probabilities are extremely low.[2]
Many philosophers don’t like fanaticism; it leads to unintuitive conclusions[3] and frankly it doesn’t feel very good to be called fanatical.
But the principles behind it are so goddamn clean — to reject fanaticism, you need to break basic axioms that have proven to be tried and true in decision making: like transitivity, continuity, independence, and more. If you walked into a bar telling people you were gonna break continuity or independence, they’d probably laugh you out as they’d explain how you are being stochastically dominated while literally money glitching you like you were an UberEats shop with a bug.[4]
So we now have a conflict between really unintuitive conclusions on the one hand and really obvious axioms on the other. In light of this conflict, should we become risk averse, losing some of the clean properties but also losing some of the really unintuitive conclusions? Do we just bite the bullet, merely accepting the very unintuitive, exploitable conclusions in edge cases? No! We should do a secret third thing… that I will be arguing for later in this post. But first, we need some background.
Principles, Decision Theory, and Moral Philosophy
Before we get into my secret third thing, we need to understand why holding onto these axioms is so important.
Decision theory has always had a good relationship with people who like to turn ‘decision data’ [5] into principles; most decision theories are relatively simple algorithms (for instance, multiply the probability of the outcome by the value for all potential actions and take the action that maximizes expected value) attempting to fit with our intuitions in lots of decisions — from whether you should bring an umbrella outside and which career you should go into [6] to questions about public health policy and finance.
Moral theory is in a similar position: simple algorithms like maximizing the utility of all sentient beings or acting in accordance with everyone’s will serve as principles that fit quite a lot of the moral data — from bystander rescue to road safety regulations.[7]
Still, these principles do not come without a cost; if you do end up with these theories (as opposed to, say, brute intuitionism[8]), you’re probably not going to fit every intuition you have perfectly, as per the cases that make philosophers call certain theories fanatical.[9]
This is how critiques to normative principles come into play: they usually come in the form of cases where our intuitions diverge from the general procedure, and this can be viewed as a trade-off: we’d like a theory to fit all of our reflected intuitions, but we also care about simplicity in our theory.[10]
This all comes back to Rawls’s concept of reflective equilibrium, which describes the way we often do and should build normative theories: by adjusting our moral principles and considered judgments until they form a coherent, mutually supportive system. The process is essentially a back-and-forth of revising principles and judgments until they align.[11]
Which brings us back to fanaticism: how much simplicity is worth tolerating extreme intuitive weirdness?
Simplicity doesn’t get infinite weight
Given this framing of principles in decision theory and moral philosophy, we learn something about the nature of these methods: simplicity doesn’t get infinite weight; in other words, we should be willing to trade off some simplicity for some number of case intuitions (or intuitions about individual cases). As you will learn in the next section, this (in my view) has implications for fanaticism and solutions to similarly structured methodological critiques. Let’s illustrate what it means for simplicity not to get infinite weight with a thought experiment:
Even our simplest moral theories like utilitarianism, for instance, come with multiple axioms [12] — individual rationality, the Pareto Principle, anonymity, and cardinal interpersonal comparisons. On the other hand, one could hypothetically accept a theory with only one or two axioms that fit with (perhaps a lot) fewer moral case intuitions. However, almost nobody really accepts or proposes these kinds of theories, showing that, while we care about simplicity, it’s not infinitely more important than other factors, so we should be willing to make some trade-off between the two.[13]
Given that simplicity doesn’t get infinite weight, there is now a question about how much weight it does indeed get… which I will totally side-step. [14] What I will say, though, is that this framing implies that there are some amount of case intuitions that can outweigh the simplicity of some theory. One implication of this is that you could potentially use different decision procedures in different cases – if the cost for diverging from that case is greater than the benefit of simplicity (for all your various normative theories), you can merely overfit the data.
In addition, if you think that some cases can be vastly more important than others (which you obviously should[15]), then there are even some cases of simplicity that can be rejected by only a very few number of case intuitions.
You can probably see where this is going, so in this same vain, let’s get into my solution to fanaticism:
My proposal to avoid fanaticism
Curve-fit the hell out of crazy-sounding, fanatical cases. Literally go like this:
Or various other variations. Here’s another:
Sorry if it’s not so clean, but maybe you should stop being such a neat freak if the cleanliness of your theory is not the end all be all.
Ok, short rant over. So what does this graph actually mean?
Without entirely describing what this graph represents (and staying agnostic about whether it indeed does entirely reflect the process of arguing for/against normative theories – in fact, I don’t believe these particular graphs do enough at capturing all the complexities[16]), you can heuristically see a line as your normative theory (whereas simplicity manifests in how straight or curvy the line is), and the amount of dots the line hits as the amount of (reflected) intuitions your theory agrees with (whereas the further your data point from the line the more costly diverging from that intuition is).[17] Then, you just minimize loss, meaning that you create some normative theory (the line) that does the best job of trading off both your weights for simplicity and explaining data.[18]
What this means for us: if you consider the costs of these fanatical edge cases to be important enough, and you think they are far enough from the outcome of your principled procedure, you can allow your decision procedure to overfit/have certain exceptions to your general rule in those fanatical-driving cases (likely when those cases are very important). [19] In other words, you can have your decision algorithm justifiably say something like maximize expected value, except when there is pascal’s mugging.[20]
Objections
Now for everyone’s favorite part of the post: criticisms and responses. Wahoo!
But this is really weird and not how we normally do normative theory, right?
Wrong![21]
I don’t think I’m alone in doing this type of view. Here are some instances where I see different well-known/popular theories doing something structurally very similar — I also think these theories can be better accounted for under the curve-fitting framework I am proposing:
- Threshold Deontology and Multi-Level Utilitarianism:
- Threshold deontology is using a rules based approach to ethics and then caring about consequences when they are too large. Multi-level utilitarianism says that we should follow rules except in certain rare situations where it is more appropriate to engage in a "critical" level of moral reasoning. In some sense, both of these theories are more complex versions of their initial forms (deontology and utilitarianism respectively) to fit more moral data (for instance, it often feels like Utilitarianism breaks too many rules in relatively low stakes-cases).[22]
- Pluralists:
- Moral pluralism accepts multiple irreducible values (justice, beneficence, liberty, etc.) instead of forcing them into one monistic framework. You can model this as, say, having a weaker weight for simplicity, using many values, and fitting a lot more moral data.
Doesn’t this just fall into permissivism?[23]
Maybe. But, in some sense, don't almost all of our normal disagreements about moral philosophy and decision theory already fall into a form of normative permissivism? [24] I mean, people accept a very very wide range of views, without clear silver bullets in any direction: think normative debates where utilitarians and deontologists shoot back and forth with ethical intuitions that don’t fit the other moral theory and disagreement about the intuition itself.
While this procedure for thinking about normative theory can answer some questions, [25] part of what it is doing is just making explicit the assumptions we were already taking for granted and having people actually argue for those views instead of accepting them on, say, vibes – perhaps this framing of normative theory can guide us to have clearer, more fruitful normative debates.
I think another critic might argue that philosophers would just throw pretty arbitrary weights post-hoc to support their already held beliefs or that the numbers chosen will often be arbitrary. I think there are two responses here: (1) some philosophers won’t [26] and (2) in the same vein as permissivism, if this framing is tracking something about the way normative theory should be done, we are indeed already throwing numbers that mean very little in these debates – only we are doing it implicitly/without proper justification. Making things explicit, then, seems to make things better.
Doesn’t this fall into intuitionism?
No – or at least, not necessarily.
An intuitionist could model their view in this framework (for example, by giving little or no weight to simplicity, or by assigning a very high cost to diverging from any intuition). But the framework itself doesn’t commit you to intuitionism. One can reject intuitionism by emphasizing simplicity — weighting simplicity heavily in theory choice. The framework can even capture something like total utilitarianism: either by giving substantial weight to simplicity or by offering an error theory (an explanation of why we have a particular intuition even if it fails to track moral facts). Graphically, this shows up when a point once thought to lie off the line is revealed, under the error theory, to actually fall on (or much closer to) the line.
Implications (or lack thereof)
I don’t think this sort of approach is actually very novel; I think people act like it all the time. Still, I don’t think it has been formalized in this way such that it can be scrutinized, and I think more work should go into this (and am happy to contribute!).
One implication is that you might get something for curve fitting like you do for risk aversion: permissiveness about how to weigh simplicity vs the strength of intuitions, etc. This is because, aside from intuitional costs which get a bit messy, there are no solidly principled ways to do this stuff — though, as this post is essentially entirely arguing, this doesn’t mean we shouldn’t.[27]
If you can get the good parts of risk aversion, without many of the bars, depending on weight for simplicity, this could make risk aversion less plausible, as there are additional theories doing getting more of the good cases and less of the bad ones.[28]
For all my effective altruists out there: one might think that this has lots of implications for giving; maybe we should care about longtermism less, maybe we shouldn’t care about shrimp welfare? I don’t think so. [29] As mentioned in a recent post by Bentham’s Bulldog, people love throwing pascal this and pascal that around when some conclusion vaguely resembles a risky wager; but in reality, we take low probability wagers all the time (seatbelts, for god’s sake)! The probability likely has to be drastically lower to be considered a pascallian wager.
If we’re already curve-fitting our theories to fit messy intuitions, maybe fanaticism isn’t a special problem at all — it just exposed the implicit methodology we were using the whole time.
We also solve decision theory and moral philosophy. Yay!
As always, let me know why I’m wrong!
(Extra seriously this time! If you’re a professional philosopher that would like to help me with this or think you have a really good objection, I would really appreciate you reaching out via DMing me here — I’m thinking about doing something like this for my thesis or gonna try to publish a fuller version in a paper.)
- ^
Also (x2), as I have been thinking about this post over the past year, I have stumbled across Ch 2 of Nick Beckstead’sPhD thesis, which does something similar, but he doesn’t take it as far as I do. While I was thinking about this post, a philosophy paper called ‘moral overfitting’ came out (in philosophical perspectives!) doing something similar as well, though it also diverges in important ways.
- ^
For all you formalists, a definition from the SEP says: “For any degree of choiceworthiness (or value, rightness, etc.) dand probability p, there is a finite degree of choiceworthiness d + such that an action has choiceworthiness d + with a probability p and is more neutral with probability (1 - p) is preferable to an action that has choiceworthiness d for sure; and there is a finite degree of choiceworthiness d - such that an action that has choiceworthiness d - for sure is preferable to an action that has choiceworthiness d with probability p and is morally neutral with probability (1 - p).”
- ^
There are these weird as heck cases when you take fanaticism to the far extremes. Pascal’s mugging (where someone says they can give you an astronomically large reward — like creating 10^50 happy lives — in exchange for something trivial, such that even though the chance of success is tiny, the expected value calculation still comes out positive), the St. Petersburg Paradox (a coin-flip game where the payoff doubles each time it lands tails before a heads, so the expected value is infinite even though no one would pay infinite money to play), and more.
- ^
Note that only some versions of rejecting fanaticism actually lead to money pumps (for instance, rounding down to zero when the probability is low enough).
- ^
We’ll define this as (on reflection) intuitive procedures or outcomes arising from decision making under uncertainty.
- ^
I.e. should I take a lower paying job at a startup with a 10% chance of huge payoff vs. a stable corporate job?
- ^
For this post, I’m going to entirely side-step the notion of reflected moral data/intuitions vs normal ones. This is not to say that it isn’t important (indeed, I think it’s extremely important), but it’s not related enough to this post to justify a more in depth explanation and caveats. Be on the lookout for this sort of article in the future, though!
- ^
Without getting into details, let’s say that brute intuitionism is just following your (reflected) intuitions.
- ^
In some sense, this is what theories are designed for, but we’ll leave this point aside for another day.
- ^
And we have the same trade-off in science!
- ^
On a point more relevant to principles, he explicitly states: “[p]eople have considered judgments at all levels of generality, from those about particular situations and institutions up through broad standards and first principles to formal and abstract conditions on moral conceptions.” When using abstract principles for reflective equilibrium, there is a question about double counting (as in, the axioms hold because of how they represent themselves in certain cases – usually in a good way – so shouldn’t using case intuitions and principles be considered double counting), but we will table this concern for this post.
- ^
Of course, you don’t have to cash out what it means to have a simple theory via literally counting up axioms; there are more traditional ways, but I used axioms for simplicity (pun intended).
- ^
Perhaps one can quibble with this trade-off by arguing that we have a satisficing view of this trade-off: whereas we only need some fitting with moral data, and after that, we start weighing simplicity a lot more (or even infinitely). This view seems implausible to me, but I will set it aside for this post and perhaps return to it in another.
- ^
For now. I plan to write more on this in the future.
- ^
Consider a simple moral theory that told us all of our intuitions in all cases except it also told us that “it was okay to torture babies because it’s fun.” Clearly, we should reject this theory even though it technically “fits more data” than most moral theories—some intuitions are just stronger and/or are more important (perhaps ones that we more commonly face are more important).
- ^
Though I do buy that normative theory building does, indeed, rely on something that at least looks like this.
- ^
This could get into questions of how one would represent certain theories being both simpler and fit the line better, but (1) perhaps this could be represented with a higher dimensional space and/or (2) perhaps it’s a reason to take the conceptual idea without the specific graphic representation seriously.
- ^
Interestingly, in the philosophy of science (and science in general), you often don’t expect your theory (line) to perfectly fit the data (points) due to noise or imperfect instruments; perhaps an analogy can be made to this case where we’d expect an ideal/correct theory not to fit all of our intuitions due to various cognitive biases affecting our moral reasoning (analogous to imperfect instruments). In that case too, we get a tradeoff between simplicity and data explanations; sometimes we expect very far outliers to be indicative of a bad theory more than true data because we expect lots of simplicity, which we may not in the normative theory case (even if we do, we do often use these overfit theories in the meantime, though), and sometimes we think it should be disregarded. Perhaps it’s about whether this outlier persists in many cases, but I will talk no further on this issue for now.
- ^
Which you probably should; giving your wallet away when someone claims they’re a wizard is probably financially bad. I’ll even let you use that as financial advice (joke - for legal reasons, nothing I say here should be taken as financial or legal advice).
- ^
One can quibble that this doesn’t tell us precisely when to start treating it as a pascal’s mugging, but we don’t know where this point is in general (as per the continuum argument). Given that we have some more precise metric for trade-offs, however, this approach might help us find that point.
- ^
Okay, maybe that’s a bit strong — I think it is weird, but it might be less weird than you might initially think but keep reading to see why.
- ^
The same can likely be said for alternatives to classical Utilitarianism like prioritarianism or averagism in population ethics.
- ^
Permissivism (in epistemology) is the view that the same body of evidence can rationally permit more than one doxastic attitude (as opposed to uniqueness, which holds that there is only one rationally justified response). A common example is subjective Bayesianism: the choice of priors or of conditional probabilities often leaves room for multiple rational credence functions, especially where precise numbers feel underdetermined. Likewise, in normative theory-building, the same metaethical or metanormative commitments may support more than one theory, given similar ambiguities (simplicity vs. fit, weight on intuitions, etc.). This need not collapse into full subjectivism—just as some Bayesians argue for objective constraints/uniqueness—but it suggests permissivism may extend into theory construction.
- ^
Perhaps this is begging the question, but interestingly, most people who accept risk aversion see it as permissive in a similar way: people don’t often argue for a uniqueness thesis/that there is only one acceptable risk preference.
- ^
In fact, in addition to helping us with fanaticism, I think it can help us with many other problems including moral uncertainty (say, by using intuitional weight as the intertheoretical comparison), metanormative ethics, and more – but more on these in later posts.
- ^
One might object: “If there is no principled way to assign numbers here, then any such assignments will be arbitrary, and thus fail to advance or clarify the underlying debates.” But I doubt this. Some metaethical views are directionally more attuned to different principles. For instance, certain views place more weight on simplicity (e.g., quasi-realism vs realism, or naturalism vs non-naturalism), whether for practical, epistemic, or conflict-management reasons. Others are more or less tolerant of noise, depending on how seriously they take evolutionary debunking arguments or how reliable they think our access to moral facts is. And views also differ on which types of data they regard as most important. In all these respects, some views seem better suited to guide principled assignments than others.
- ^
Seriously. If this was your big objection, you haven’t been paying enough attention.
- ^
One reason you might still like risk aversion more than this is if you think overfitting in cases is much worse than adding additional principles that do the work – perhaps because, as I’ve said before, we often see outliers like that in science to be a good reason to reject the theory in its totality.
- ^
Maybe it is so if your cause prioritization relies on the many digital nematodes in the very far future such that you can only make a directional effect, and it’s 49% likely to create as much damage as benefit.

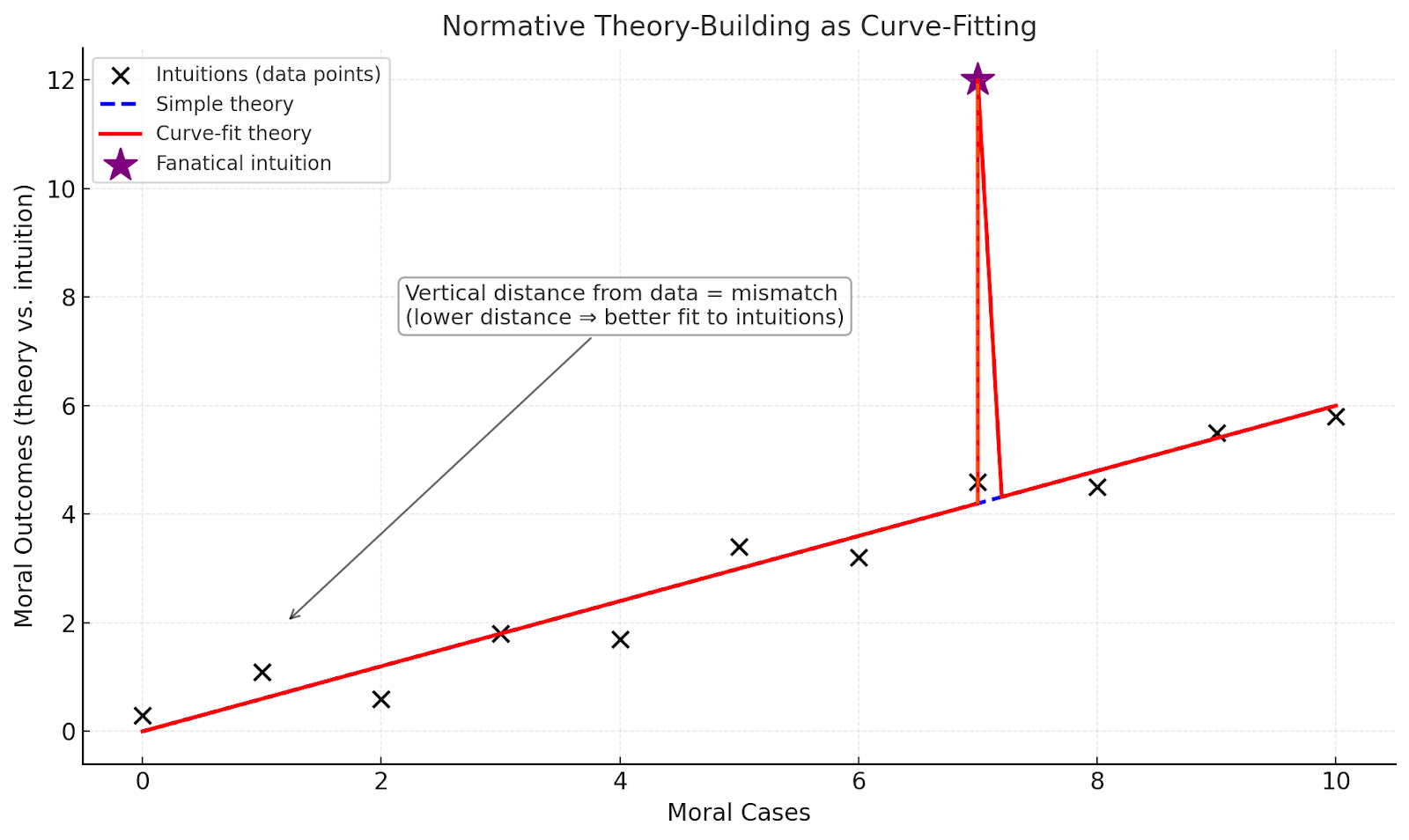
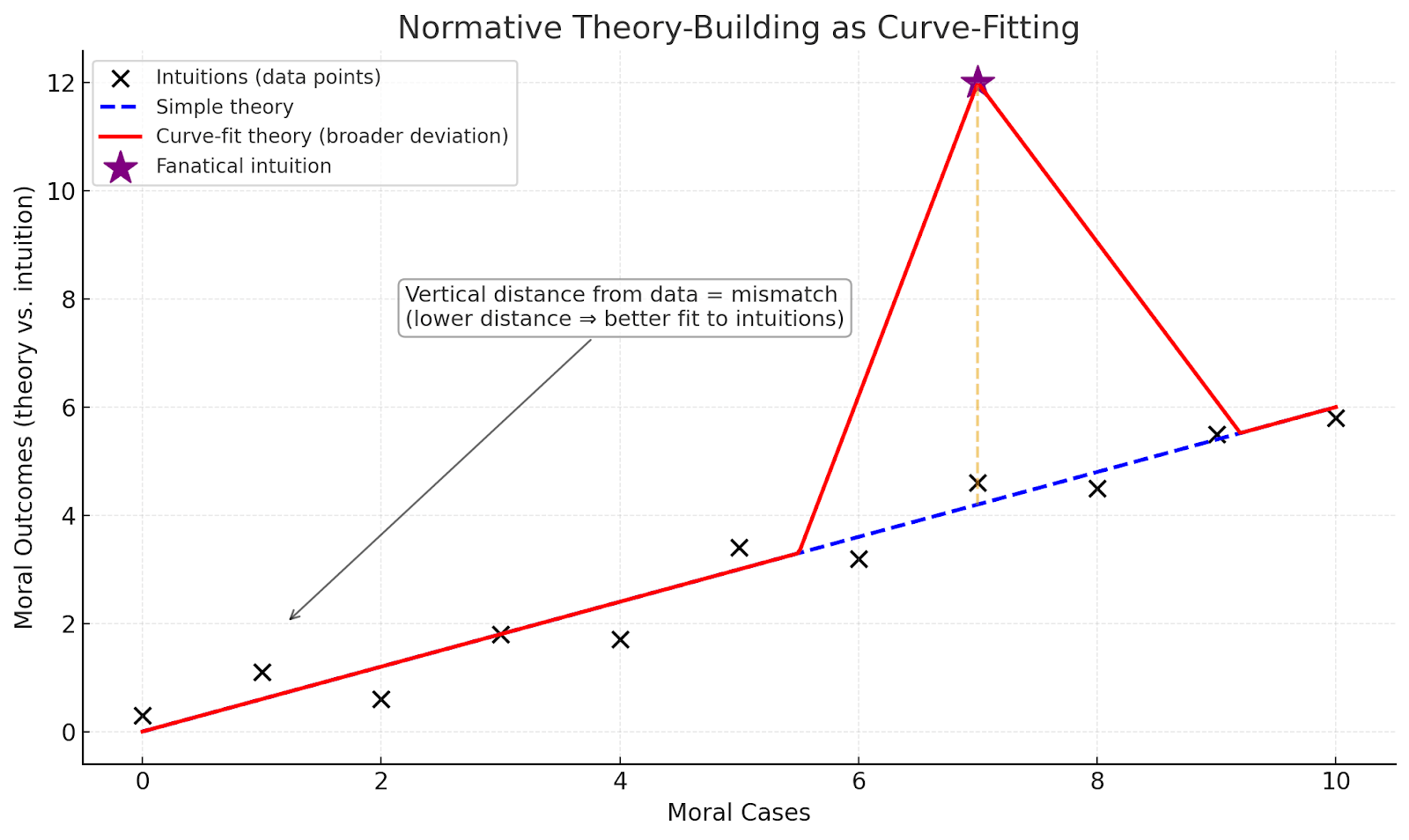
I don't get how you're actually proposing doing curve-fitting. Like, the axes on your chart seem fake, particularly 'moral cases'. What does 2 vs 8 'moral cases' mean? What is a concrete example of a decision where you do X without curve fitting, but Y with curve fitting?
Without an actual mathematical formalization or examples, I struggle to see what your proposal looks like in practice. This seems like another downside relative to threshold deontology, where it is comparatively intuitive to see what happens before and after the threshold.
Sorry if it wasn't clear -- this is literally just the moral case intuition, and the numbers are just meant to reflect another moral intuition that your curve can either align with or not.
Some concrete decision would be based on how one weights simplicity mathematically vs fitting data, etc. I wanted to stay agnostic about it in this post.
I think I disagree with this last point in that -- it looks like threshold deontology is doing something like I am (in that it is giving two principles instead of one to fit more data), but it is often not cashing it out this way which makes it hard to figure out where you should start being more conseqentialist. One interpretation of what this proposal does is it makes it more explicit (given assumptions), so you know exactly where you're going to jump from deontic constraints to consequences.
Like I said in the post, I think that this graph definitely doesn't reflect all the complexities of normative theory building -- it was a mere metaphor/ very toy example. I do think that even if you think the graphic metaphor is merely that (a metaphor), you can still take my proposal conceptually seriously (as in, accept that there's some trade-off here, and plausibly case intuitions can outweigh general principles.
I don't think that the intuition behind 'curve fitting' will actually get you the properties you want, at least for the formalizations I can think of.
How would you smooth out a curve that contains the St. Petersburg paradox? Simply saying to take the average of normal intuition and expected-value calculus (which you refer to as fanaticism) doesn't help. EV calculus is claiming an infinity. I'm not aware of curve fitting approaches that give understandable curves when you mix infinite & finite values.
Plus, again, what dimensions are you even smoothing over?
The curve is not measuring things in value but rather intuitive pull according to this data--simplicity trade-off!
Executive summary: This exploratory post argues that we should avoid fanaticism in moral philosophy and decision theory not by breaking core axioms or accepting bizarre conclusions, but by “curve-fitting” — allowing our theories to include exceptions for extreme, fanatical cases when the cost of ignoring intuitions outweighs the value of simplicity.
Key points:
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.