(This post will be much easier to follow if you’ve first read either “Should you go with your best guess?” or “The challenge of unawareness for impartial altruist action guidance”. But it’s meant to be self-contained, assuming the reader is familiar with the basic idea of cluelessness.)
According to the view that we’re clueless, the far-future consequences of many of our actions are so ambiguous that we can’t say if they’re good, bad, or neutral in expectation. Concerningly, this view doesn’t even let us say that the most obviously bad actions are, well, bad. I’ll show how we can take cluelessness seriously and still rule out these actions in a principled way.
To see the worry, consider this story. You’re a fairly thoughtful longtermist who one day comes across the idea of cluelessness. You’re skeptical, but you find yourself grudgingly agreeing that predictions about the far future are mostly made-up. Claims like “this intervention will increase expected total welfare across the cosmos” start to seem fake. Still, surely some actions have better or worse consequences than others? Soon enough you wonder if that thought is fake too. You realize that even, say, kicking a puppy could prevent human extinction. Maybe this act of pointless cruelty sparks moral outrage in some onlooker, galvanizing them to work a bit harder at their AI safety job. Yes, this possibility is clearly far-fetched. And you can easily imagine stories pushing in the opposite direction. But you can’t come up with a good argument that the expected long-run effects point one way or the other, or that they precisely cancel out. (That is, your cluelessness is “complex”, not “simple”.[1]) The sign of the EV of kicking the puppy seems to be: shrug. You walk away feeling like this reasoning is too clever by half, even if you can’t say where exactly it went wrong. So you decide to file cluelessness under “yeah I get the arguments, but this is a bridge too far”. And you go back to thinking about how to solve AI alignment.
More generally, here’s what this tale illustrates. As argued in Mogensen (2020) and this sequence, impartial consequentialists[2] can’t say whether any intervention has higher or lower expected value than inaction. At least, not without arbitrarily setting our degrees of belief in far-future outcomes. So all interventions’ expected total consequences are incomparable with inaction — neither better, worse, nor equally good. But by this logic, impartial consequentialists will just as well end up clueless about every moral choice, including excruciatingly obvious ones. Call this troubling implication radical cluelessness.
Radical cluelessness poses two big problems. First, it’s clearly a huge bullet to bite! We might respond, “I just shouldn’t kick the puppy because that’s common sense.” Yet this seems ad hoc. If we default to “common sense” here, it’s not clear how to make decisions in general, and on what basis. Maybe we could reject impartial consequentialism and non-arbitrary empirical beliefs to get the desired conclusion, but that, too, looks gerrymandered.
Second: A promising response to the first problem is to appeal to normative uncertainty or pluralism. After all, views that imply radical cluelessness (“clueless views”) don’t tell us whether to kick the puppy, so other views we’re sympathetic to should break the tie (see, e.g., Vinding and here; more below on what I mean by a “normative view”). However, it’s not trivial to make sense of this reasoning with a rule that’s sensitive to differences in the stakes of a choice for different views. Indeed, MacAskill (2013) argues that “tiebreaking” violates stakes-sensitivity in choices among more than two options.[3] He instead recommends ranking actions by their expected “choiceworthiness” (roughly, the degree to which the action is approved by each view; MacAskill and Ord 2018). But then, since the clueless view says all actions have incomparable choiceworthiness, this view “infects” the whole calculus. That is, all actions end up with incomparable expected choiceworthiness. MacAskill et al. (2020, Ch. 6) give a response to this problem, but it doesn’t work when we have high weight (e.g., credence) on clueless views — as it seems we should, given the strong arguments for cluelessness.
In this post I’ll present a choice rule under normative uncertainty that avoids radical cluelessness, without (1) making ad hoc appeals to common sense or (2) violating stakes-sensitivity.
I call this choice rule metanormative bracketing. The core idea, which adapts Kollin et al.’s (2025) “bracketing” proposal to normative uncertainty, is simple: Suppose we have some weight on normative views that say and are incomparable, and some weight on views that (in aggregate) prefer . We make our decision based only on the aggregate verdict of the latter views, “bracketing out” the former, and thus choose . For example, you might reason, “All the non-clueless views I put weight on, like ‘follow your conscience’, prohibit kicking the puppy. Clueless views don’t tell me to kick it. So I won’t.”
That sounds a lot like the “tiebreaker” reasoning above, so what takes work is showing that we avoid (1) and (2) above. Briefly, I’ll argue:
- Avoiding ad hoc-ness: Unlike “just don’t do common-sensically evil things”, metanormative bracketing is a general, principled choice rule. There’s an independent motivation for applying bracketing to normative views, and for bracketing out clueless views. (Moreover, we needn’t put artificially low weight on clueless views to prohibit obviously unacceptable actions, unlike with MacAskill et al.’s (2020, Ch. 6) approach.)
- Respecting stakes-sensitivity: Since we can still aggregate the verdicts of the views that we don’t bracket out, metanormative bracketing is stakes-sensitive in binary choices. And, metanormative bracketing can avoid MacAskill’s (2013) objection above. For example, we can use an analogue of the Borda rule (MacAskill 2016) to choose among more than two actions in a stakes-sensitive way.
Notably, while metanormative bracketing sets aside clueless views in decision-making, I’ll argue that this differs in practice from ignoring (or wagering against) cluelessness per se.
Summary:
- Suppose we endorse impartial consequentialism, combined with minimally arbitrary approaches to forming beliefs and making decisions. Then, we seem unable to compare the goodness of any pair of actions in practice. (Under some versions of an alternative decision theory called “bracketing”, we can avoid this conclusion. Unfortunately, this isn’t true of the versions with the strongest independent motivation.) (more)
- We’d like our choice rule under normative uncertainty to be stakes-sensitive. But according to the leading stakes-sensitive rules, such as variants of maximizing expected choiceworthiness (MEC), incomparability under clueless views leads to incomparability overall. (At least, that is, if we put sufficiently high weight on clueless views.) (more)
- With metanormative bracketing, we use a stakes-sensitive rule to aggregate the verdicts of subsets of our full set of normative views. Given a pair of actions, we look at which sets of views in aggregate prefer one action over another — call these “bracket-sets”. Then, if all the “largest” bracket-sets favor over , we prefer overall. (more)
- Why apply bracketing at the level of normative views, rather than something more fine-grained? Because metanormative reasoning itself works by first looking at individual normative views’ verdicts, then putting them together into an overall verdict. (more)
- Given more than two options, first, we rule out actions that are dispreferred in a stronger sense that I’ll make precise. Second, for each pair of remaining actions, we calculate the difference in choiceworthiness under the largest bracket-set. And we take the action with the greatest sum of these pairwise differences. (more)
- Because we can bracket out clueless normative views, and the remaining views will disprefer the most obviously immoral actions compared to some alternatives, metanormative bracketing prohibits such immoral actions. (more)
- One implication of metanormative bracketing is that we should be less inclined to reject minimally arbitrary epistemology, since that’s not necessary to avoid radical cluelessness. As for other implications, we might favor acting on views that imply longtermism, because they’re in some sense “higher-stakes”. I’m not confident this is misguided. But I currently think metanormative bracketing favors acting on minimally arbitrary beliefs plus consequentialist bracketing, which imply neartermism, because they’re grounded in stronger reasons. (more)
The problems and why previous work doesn’t fully solve them
Let’s unpack the motivating concerns from the first two summary points above.
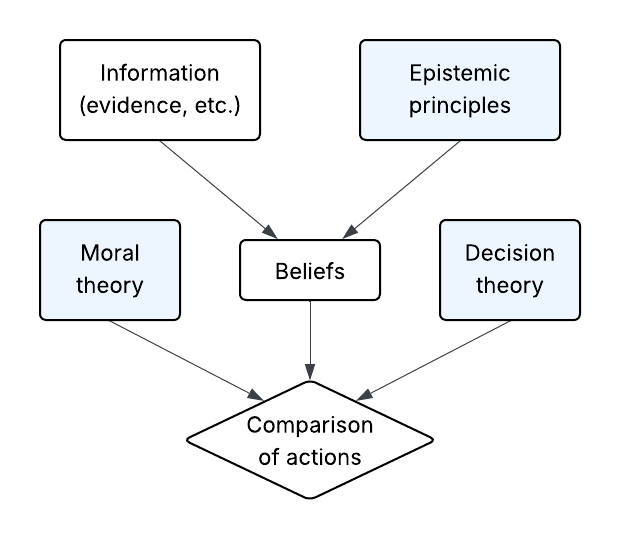
First, though, this post will talk a lot about “normative views”. What does this mean? Informally, a normative view is a combination of a moral theory, epistemic principles, and a decision theory. That is, it’s the package of standards by which a decision-maker might compare actions, given their available information. See Fig. 1. (I’ll say that a normative view “features” each of these three components, e.g., the clueless view below features some kind of impartial consequentialism as its moral theory. Also, see this post for background on why the rationality of beliefs depends on normative principles.)
Problem 1: Radical cluelessness due to indeterminate beliefs
I’ve argued previously that a highly compelling normative view — impartial consequentialism combined with certain epistemic principles and decision theory — leads to radical cluelessness (see also Mogensen (2020) and Kollin et al. (2025, Sec. 2 and 7)). Here’s the barebones case for that claim.
According to epistemic principles that aim to avoid arbitrariness, our degrees of belief about the possible far-future outcomes of our actions should be indeterminate. That is, instead of precise probabilities, imprecise probabilities (a set of distributions ) are a better model of these beliefs. Hence, the difference between the “expected total value” of actions and should also be imprecise, represented as the set of for each in the set . And, per the maximality decision theory, we should prefer over if and only if every is positive.
But far-future consequences depend heavily on novel, complex pathways, many of which we haven’t even conceived of. Because of this, our beliefs end up so severely indeterminate that for any pair of actions, we can’t pin down a set of EV differences that’s all positive or all negative. Thus it seems that (practically) all actions are incomparable under standard impartial consequentialist views, hence they’re all permissible.
Optional technical example 1.
Consider this toy formalization of the problem, in terms of the puppy example from the intro:
- Suppose that if you kick the puppy, with some small probability a bystander working in AI safety will be motivated to work a bit harder.
- Since it’s very unclear how to weigh the consequences of this person’s job on net x-risk, you’re deeply uncertain whether the bystander working harder would increase x-risk (event ) or decrease it (event ). You represent your beliefs with a set , such that your credence in is the interval .
- Say that:
- kicking the puppy would decrease the puppy’s welfare by 1;
- decreased x-risk would increase the total welfare of everyone else by [Big Number] in expectation; and
- increased x-risk would decrease the total welfare of everyone else by [Big Number] in expectation.
Then the difference in expected total welfare between kicking the puppy vs. not kicking it is . This interval contains both positive and negative numbers if is big enough, so according to maximality, kicking the puppy is incomparable with not kicking it.
What if we still endorsed impartial consequentialism and indeterminate beliefs, but had a more discriminating decision theory than maximality? Kollin et al. (2025) develop one such decision theory, which I’ll call consequentialist bracketing.[4] Very briefly, the intuition is that in the puppy example, we could reason like: “On one hand, I’m clueless about the effects of kicking the puppy on everyone else besides the puppy. This doesn’t give me a reason to choose either action. On the other hand, I’m not clueless about the fact that kicking the puppy makes the puppy worse off. This gives me a reason not to kick the puppy. Overall, then, I have more reason to choose ‘don’t kick the puppy’.”
I’m sympathetic to this idea (more on that later). However, the problem comes in when we get precise about the individual units that make up “everyone else” — are they persons? Units of spacetime? Something else? As explained in much more detail by Clifton, it turns out that under the most morally well-motivated answers to that question, consequentialist bracketing will still imply radical cluelessness.[5]
Problem 2: Tradeoff between infectious incomparability and stakes-insensitivity
Even if clueless normative views are highly plausible, intuitively the non-clueless views we give weight to should still give us action guidance. But as I’ll show next, standard decision rules under normative uncertainty don’t resolve radical cluelessness. And an alternative approach that does avoid radical cluelessness has another serious problem.
In a popular approach to decision-making under normative uncertainty, we represent each normative view as assigning actions cardinal degrees of choiceworthiness. Then, we maximize expected choiceworthiness (MEC), where the “expectation” is with respect to our weights on different views (MacAskill and Ord 2018). The clueless view assigns each action a set of expected values, that is, the expected value under each distribution in the set representing our indeterminate beliefs. So our actions don’t have precise choiceworthiness. How do we generalize MEC to this case?
One natural generalization is: Find each action’s expected choiceworthiness given each distribution in . Then, prefer to if and only if has higher expected choiceworthiness than under every .[6]
Here’s the snag. If an action’s expected total value according to the clueless view is severely indeterminate, then we’ll have severely indeterminate expected choiceworthiness, too (see example below). And so all actions will end up incomparable under the generalization of MEC as well! This is “infectious incomparability”. MacAskill et al. (2020, Ch. 6) propose a way around this,[7] which works if we don’t have high weight on a clueless view. But as noted in the previous section, there are strong independent motivations for clueless views, so we can’t rely on their proposal.
Optional technical example 2.
Consider the case in Table 1, adapted from MacAskill et al. (2020, Ch. 6). We put weights and on a non-clueless and clueless view, respectively. And given our set of distributions , we have a range of values for a parameter .
Table 1. Choiceworthiness values for two actions under two normative views, for some much smaller than 1. The actions are incomparable under the clueless view.
| : Non-clueless | : Clueless ( in ) | |
|---|---|---|
On the clueless view, has higher choiceworthiness than under , and the other way around under . Given that and are therefore incomparable under the clueless view, while under the non-clueless view is better, intuitively we should choose . As long as we put more weight on the clueless view (i.e., ), though, has lower expected choiceworthiness under .
Perhaps, instead, we shouldn’t aggregate the clueless and non-clueless views together as MEC does. Elkin (2024) proposes this approach: Say we have weight 0.9 on a view that permits both and , and weight 0.1 on a view that only permits . Intuitively, each action should get as many “approval votes” as our total weight on views that permit it. So since gets 0.9 votes while gets 1, we choose . Then, even if we put a lot of weight on a clueless view (which approves every action), we’d choose the action most approved by the non-clueless views.
Approval voting only considers which actions a normative view permits, not the actions’ degree of choiceworthiness. But ideally, our theory of choice under normative uncertainty should be stakes-sensitive. The classic example to illustrate this property is, say you’re uncertain between a view that gives shrimp very little moral weight, and a view that gives shrimp significant moral weight. And you’re deciding whether to buy a meal containing shrimp (based only on near-term effects). Even if you’re highly confident in , the minor benefit to yourself of eating shrimp with respect to seems much smaller than the major moral harm of eating shrimp with respect to , so arguably you shouldn’t eat the shrimp. Yet approval voting violates stakes-sensitivity: if you put (e.g.) weight 0.51 on view and eating shrimp would give you more pleasure, approval voting recommends eating shrimp.
(It’s possible that some stakes-sensitive alternatives to MEC in the literature avoid infectious incomparability, but I suspect the problem generalizes.)
Metanormative bracketing
To recap, the puzzle is:
- We should put high weight on a normative view that implies radical cluelessness. (Consequentialist bracketing, while promising, doesn’t avoid cluelessness under the most natural ways to individuate “consequences”.)
- If we want our choices under normative uncertainty to be stakes-sensitive, the above apparently implies we’re also radically clueless overall.
In response, we’ll apply bracketing to normative views, rather than consequences. In this section, I’ll first set up the necessary technical machinery (more), and argue that metanormative bracketing (mostly) avoids consequentialist bracketing’s individuation problem (more). Then I’ll present a metanormative bracketing choice rule (more), and show how it avoids radical cluelessness while allowing for stakes-sensitivity (more; more).
Setup
To make my claims precise, I’ll now get somewhat more formal than the previous discussion, but here’s a tl;dr:
- We put weight on multiple normative views, each of which compares actions’ choiceworthiness. We’ll assume very little else about the structure of normative views.
- We have some base rule for aggregation across views (e.g., our imprecise generalization of MEC above), which can be stakes-sensitive. This rule compares actions’ aggregate choiceworthiness over any subset of our full set of views.
- Then, for any pair of actions, a metanormative bracket-set is a set of normative views that, when aggregated, prefer one action over the other. As a first pass, if there’s a unique largest bracket-set, we should at least prefer over overall if is preferred under that bracket-set.
We have sets of candidate actions , normative views , and weights on the normative views, which we’ll assume to be precise numbers for simplicity.[8] Each view in is a way to compare two actions’ choiceworthiness. We’ll write (resp. ) to mean “view says is more choiceworthy than (resp. at least as choiceworthy as) ”. For example, according to a clueless view , it’s neither true that “kick puppy” “don’t kick puppy” nor that “don’t kick puppy” “kick puppy”.
(It’s not clear what the set should be exactly. Maybe we should count some view as two sub-views, or maybe not. More on this later.)
We’ll assume as little as possible about these normative views. In particular, first, you don’t have to interpret them as all-things-considered theories you’re uncertain over, with representing credences. Instead, you might have a pluralistic all-things-considered theory composed of different views (Hedden and Muñoz 2024), with representing your weights on these views. Second, the degrees to which normative views consider actions choiceworthy (e.g., expected utilities) might be comparable across some views. In the shrimp example above, say, we put the choiceworthiness of eating shrimp under the “shrimp have high moral weight” view on a common scale with choiceworthiness under the “low moral weight” view. But we won’t assume all normative views assign comparable degrees of choiceworthiness.
We’ll then take any approach to aggregating verdicts of normative views we like, including stakes-sensitive rules like MEC. This is our “base rule”, which compares a pair of actions’ aggregated choiceworthiness over any subset of our set of views . We’ll write to mean “the aggregated choiceworthiness over (weighted by ) of is greater than ”.[9] For some subsets , our aggregation rule will also tell us the cardinal difference in aggregated choiceworthiness over between and . (This could be either a precise number or an interval.) If so, we’ll write that difference as .
Optional technical example 3.
Take the puppy example again, where is “kick the puppy” and is “don’t kick the puppy”:
- Suppose you put weight 0.9 on “impartial consequentialism plus indeterminate beliefs plus maximality”, and weight 0.05 each on “impartial consequentialism plus indeterminate beliefs plus consequentialist bracketing” and “follow your conscience”.
- Assume this variant of consequentialist bracketing is operationalized so that only the puppy’s welfare is bracketed in.
- And assume and are intertheoretically comparable. Specifically, the differences in choiceworthiness between and that they assign are given by, respectively, the difference in expected total value and difference in bracketed-in expected value. Then, the choiceworthiness difference according to is , while the choiceworthiness difference according to is .
- So, prohibits kicking the puppy. Since clearly also prohibits kicking the puppy, . What happens when we aggregate each of these two views’ verdicts with that of ?
- :
- Since we put weight 0.9 on and 0.05 on , we have .
- We thus have infectious incomparability: is incomparable to with respect to .
- :
- It’s not clear how to intertheoretically compare this view with . Again, though, it seems that any reasonable stakes-sensitive aggregation rule would conclude that is incomparable to with respect to , and therefore with respect to .
- :
It seems, then, that we should choose (“don’t kick the puppy”). Because , and adding to either or both of these two views would result in incomparability.
We can now define the key building blocks for our extension of bracketing to normative uncertainty, borrowing Kollin et al.’s (2025) terminology. In consequentialist bracketing, we looked at whether, by restricting attention to some subset of moral patients, we could compare actions’ expected total value. Likewise, we can check whether restricting attention to some subset of normative views lets us compare actions’ aggregated choiceworthiness:
Metanormative bracket-set. A metanormative bracket-set relative to actions and is a subset of such that, with respect to aggregated choiceworthiness over , the actions are comparable. That is, either or .
(I’ll write “bracket-set” for simplicity.) In the example above, the bracket-sets are , , and .
And, as in the consequentialist case, intuitively we’d like to aggregate as many normative views as we can while maintaining comparability. Thus we’re interested in:
Maximal metanormative bracket-set. is a maximal metanormative bracket-set if is a bracket-set and there’s no bracket-set that strictly contains .
The unique maximal bracket-set in our example is . This is the easiest case: If we only have two actions to compare, and a unique maximal bracket-set, then there’s a clear intuition that we should choose the action favored by the maximal bracket-set. We “bracket out” the views outside that set.
Happily, we’ve avoided the key problem with approval voting. In choices between two actions, as long as our base aggregation rule is stakes-sensitive, then so is the rule in bold above. E.g., if we had also put high weight on a clueless view in our example about shrimp, then the maximal bracket-set under a stakes-sensitive would still prohibit eating shrimp. That said, we haven’t guaranteed stakes-sensitivity in choices among more than two actions — which MacAskill (2013) argues is violated by a principle similar to metanormative bracketing, called “Dominance over Theories”. We’ll come back to that later.
Does metanormative bracketing have an individuation problem?
(Thanks to Kuutti Lappalainen and Clare Harris for very helpful discussion on this point, and to Kuutti for the virtue ethics example.)
Before moving on, we should revisit our worry about consequentialist bracketing. Whether that approach avoids radical cluelessness depends on a potentially arbitrary choice of how to individuate the “consequences” that we bracket over. Does metanormative bracketing avoid analogous problems?
Yes and no. Fortunately, it doesn’t seem that we could just as well bracket over “choiceworthiness on behalf of each moral patient” or “choiceworthiness on behalf of each unit of spacetime” (as in the case of consequentialist bracketing). That’s because the structure of metanormative reasoning suggests a unique unit to bracket over: normative views.
While this may seem intuitive, it’s worth checking carefully:
- When we make our all-things-considered choice (via metanormative reasoning), we’re adjudicating between different ways of comparing actions’ choiceworthiness. E.g., we’re asking what “impartial consequentialism plus indeterminate beliefs plus maximality” says about each action, what “impartial consequentialism plus classical Bayesian epistemology and decision theory” says, and so on. We aren’t judging each action directly, without any further structure. So there’s a principled motivation for bracketing over normative views.
- To see how this will help us avoid radical cluelessness, suppose we claimed, “Based on our beliefs under a clueless view, there’s some strong reason to kick the puppy: doing so might greatly benefit some possible people in the far future. Thus we still have radical cluelessness.” This wouldn’t make sense under metanormative bracketing, because there’s no remotely plausible “normative view” that says the overall balance of reasons favors kicking the puppy. Instead, the clueless view as a whole gives us no reason to choose either way, so we bracket it out.
Yet, there isn’t an obvious privileged way to individuate normative views. For example, say you’re deciding whether to take some honest yet disloyal action, based on a kind of virtue ethics. Are you following one unified “virtue ethics” view? Or are you putting some weight on an honesty-prioritizing view, and some weight on a loyalty-prioritizing view? And what if every maximal bracket-set under the first approach to individuation says , while some maximal bracket-sets under the second approach say ? (See Appendix for an example.) I’ll leave it to future work to assess how much of a problem this is in general. In this post, I’ll focus on showing that bracketing over normative views avoids radical cluelessness no matter how we individuate views.
Relatedly, we might worry that it’s ad hoc to infer “the clueless view gives us no reason to choose” from “the clueless view says the relative choiceworthiness of and is indeterminate”. Should we rather say the clueless view gives us an indeterminate reason to choose, and so we still can’t resolve infectious incomparability?[10]
I think the reasoning we just went through supports the “no reason” perspective: Metanormativity is a different level of analysis than first-order normativity. If view doesn’t consider more or less choiceworthy than , it seems natural to say that doesn’t “have a complaint” against choosing either or . And thus, ’s verdict has no weight in the choice between and .
A full metanormative bracketing choice rule
There are many different ways we could generalize “choose ‘the’ action favored by ‘the’ maximal bracket-set” to other cases. For example, if the maximal bracket-sets and for a pair of actions disagree on which action is required, but there’s more at stake under than , perhaps we should go with the action required by .
To keep things simple, I’ll focus on one (relatively permissive) choice rule that:
- avoids radical cluelessness, and
- satisfies stakes-sensitivity in choices among three or more actions, at least in “easy” cases. (The way we’ll do this here is merely one example. There might be better approaches.)
Accordingly, the rule has two steps. Roughly: First, we’ll prohibit the most obviously bad options. Second, we’ll rank the remaining options in a stakes-sensitive way, by scoring each option based on how much it beats the alternatives under their maximal bracket-sets.
Step 1: Ruling out the worst options
To start, when we’re comparing two actions, we should prohibit an action that all the maximal bracket-sets agree is worse:
Bracketing dominance. Action bracketing-dominates if, for all maximal bracket-sets for and , we have .
However, in some decision problems this relation will give us a cycle, dominates dominates dominates (example below). Then if we naïvely compare each pair of actions and rule out anything that’s bracketing-dominated, we could end up prohibiting every action. That’s, well, not exactly action-guiding.
To get around that, we’ll start by prohibiting actions that are dominated in a stronger sense:
Covering. Action covers if (1) bracketing-dominates , and (2) for every other action that bracketing-dominates, also bracketing-dominates .
If we endorse bracketing-dominance as an expression of our pairwise preferences between actions, then at least prohibiting covered actions seems pretty reasonable. After all (to put it loosely), if is covered, then some alternative can do everything can do and more. (See Fig. 2 below for examples.) And at the same time, if our only options are in a cycle as above, none of them are covered, so they’re all permissible at this step.
Step 2: Stakes-sensitively ranking the remaining options
On its own, “don’t choose covered actions” is a rather permissive rule. To narrow things down further in a stakes-sensitive way, if possible, we’ll score each action using a rule inspired by weighted Borda scoring (MacAskill 2016), which I’ll call “bracketing Borda scoring”. (This is just meant to be one example of a stakes-sensitive rule we could use. We might consider other rules, perhaps from this list.) See next section for the precise definition. For now, I’ll illustrate the idea with an example adapted from MacAskill’s (2013) counterexample to Dominance over Theories (recall above).
Suppose we have three actions , where dominates dominates dominates . (Even if each normative view’s ranking is transitive, we can have a cycle when we have different maximal bracket-sets for different pairs of actions.) And suppose the minimum difference in aggregated choiceworthiness under the maximal bracket-set for — call this the margin of victory of over — is much larger than for or . Intuitively, then, we should choose . We get this result if we do the following: Score each action by the sum of its margins of victory against each uncovered alternative. Then rank the actions by these scores. See below for the more formal example.[11]
Optional technical example 4.
Consider Table 2. We put weights of 0.01 and 0.99, respectively, on two normative views and , which feature the same epistemic principles but a different moral theory. We’ll suppose these views assign intertheoretically comparable degrees of choiceworthiness, so our aggregation rule simply takes the expected choiceworthiness over the two views. Our indeterminate credence in some world-state is .
Table 2. Choiceworthiness values for three actions under two normative views. For the pairs of actions and , the actions are incomparable under and . But is more choiceworthy than under .
| : | : ( in ) | |
|---|---|---|
For each pair of actions , we’ll find its maximal bracket-set and the difference in aggregated choiceworthiness under that bracket-set. The margin of victory of over (which can be negative, if is dispreferred to ) is the minimum value of over the values of . Then we have:
- , and ;
- , and ;
- , and .
The bracketing Borda scores are therefore:
- :
- :
- :
This method gives us the ranking , the intuitive result.
Summary of the choice rule
Altogether, then, here’s the proposed rule, given candidate actions , normative views , weights , and a base aggregation rule :
- Prohibit all covered actions.
- Check if, for all pairs in the set of uncovered actions, we have a unique maximal bracket-set such that there exists a cardinal difference in aggregated choiceworthiness (and these values are all intertheoretically comparable).
- If so: Permit only the uncovered actions that maximize the bracketing Borda score .
- If not: Permit all uncovered actions.
Why metanormative bracketing avoids radical cluelessness
Now, what does all this buy us? Let’s consider the most obviously immoral (hereafter, “immoral”) actions, that is, actions that intuitively should be prohibited by our choice rule no matter how clueless we are about the consequences. If we want to say that an immoral action is prohibited, it’s enough to argue that this action is covered.
And that’s easy to show! Let be any immoral action, and be any non-immoral action. Then it’s fair to assume that according to any reasonable aggregation rule, is more choiceworthy than under each maximal bracket-set. That’s because, suppose there’s some subset of views that perversely says . Among the non-clueless views, we’ll have more weight on views that say (e.g., non-consequentialist rules, or “follow your conscience”) than . (And it’s implausible that according to the perverse views, would be so much more choiceworthy than as to cancel out these views’ lower weight.) This also seems to be true no matter how we individuate normative views. So would bracketing-dominate . And this is true of every pair of non-immoral and immoral actions. Therefore, assuming of course we don’t deem every action immoral, each immoral action is covered by a non-immoral action.
Implications of metanormative bracketing
While prohibiting actions like kicking a puppy is common sense, the metanormative bracketing framework shows how to preserve this intuition in a non-ad hoc, stakes-sensitive way. What less obvious things might this framework imply?
Cluelessness and cause prioritization
For one, we have a way to avoid the most crazy upshots of consequentialist cluelessness in our overall decision-making, without needing to reject indeterminate beliefs. This defuses the reductio against indeterminate beliefs based on their practical conclusions. So, we should instead assess such beliefs on their own (epistemological) merits.
And, puppy-kicking aside, suppose we think it’s also a “crazy upshot” of cluelessness to be silent on local consequentialist moral judgments — like, “when you can either save one or two children drowning in a pond, save two (even at a greater cost to yourself)”.[12] We might genuinely endorse this intuition, even though we know we’re clueless about the expected consequences. If so, maybe this is because we put some weight on a decision theory like consequentialist bracketing. (Even if it’s not neatly fleshed out.) This can be action-guiding even if, due to the individuation problem, we don’t put high weight on consequentialist bracketing in absolute terms.
Putting these points together: Since I find impartial consequentialism and indeterminate beliefs very well-motivated, and these combined with consequentialist bracketing seem to imply neartermism (as Kollin et al. (2025) argue), I think it’s plausible that metanormative bracketing implies neartermism.
On arbitrariness and neartermism vs. longtermism
By this point, though, you may be thinking something like:
“Your argument against radical cluelessness seems to appeal to our kinda-arbitrary ‘conscience’. And just now, you appealed to the kinda-arbitrary framework of consequentialist bracketing. What if we also put some weight on views that feature kinda-arbitrary precise beliefs or EV comparisons, i.e., views that imply longtermism? These views are much higher-stakes, so they should primarily guide our decisions. So doesn’t metanormative bracketing have the same practical implications as if we’d simply rejected the arguments for cluelessness, and stuck with longtermism?”
The answer depends on your weights on these different views, and how you do intertheoretic comparisons of choiceworthiness. It doesn’t seem obviously unreasonable to favor longtermism under metanormative bracketing. But here’s why I don’t.[13]
To start, why would we consider a longtermist view “much higher-stakes” than a neartermist view (i.e., impartial consequentialism plus indeterminate beliefs plus consequentialist bracketing)? Presumably, the reasoning is:
- “Take a longtermist intervention and neartermist intervention . Based on a longtermist view, what makes more choiceworthy is the astronomically greater expected aggregate welfare resulting from compared to .
- “Based on a neartermist view, what makes more choiceworthy is the greater, but not astronomically greater, expected bracketed-in welfare resulting from .
- “Therefore, the difference in choiceworthiness under the longtermist view, , is astronomically greater than the difference under the neartermist view, . (These choiceworthiness differences are the ‘stakes’.) Thus should dominate our decision-making, even if we have low weight on .”
However, this reasoning assumes the two views’ expected welfare differences are already on the same scale. The “expectations” used in the longtermist vs. neartermist views are justified by qualitatively different reasons (more on this in the list below). This means we can’t immediately translate the expected welfare differences into intertheoretically comparable choiceworthiness differences. Rather, we also need to look at the reasons that ground these numbers. Only then can we say whether is greater than .
(I’m not saying that is, e.g., the product of a raw “stakes” quantity and a strength-of-reasons quantity. Rather, because of the qualitative distinction between the reasons that ground the and numbers, I think the way we compare these choiceworthiness differences should itself be qualitative!)
As a loose analogy, consider the difference between assigning a credence of 50% to (a) “this apparently unbiased coin will land heads”, vs. to (b) “AI will disempower humanity”. Even assuming the 50% credence in case (b) is reasonable, and even though the credences in both cases are identical, the reasons for the 50% credence in case (a) seem a lot stronger.
Similarly, I find the reasons behind a neartermist view’s choices stronger than those of a longtermist view — holding my weights on these views fixed. Let’s look at which kinds of reasons could ground longtermism. I don’t think any of them provide a solid basis for my decisions:
- Precise beliefs: “We should have precise beliefs, so longtermist action has higher EV than alternative .”
- My colleague Jesse Clifton and I have argued previously that the intuitions in favor of precise Bayesian epistemology, or similar, are confused (here and here).[14] The problems for these intuitions run deep enough, I think, that precise beliefs don’t seem like the kinds of “beliefs” that provide strong reasons for choice.
- Imprecise EV comparisons: “We should have not-too-severely indeterminate beliefs, or somehow aggregate the interval of EV differences between and , so longtermist action is better than alternative .”
- To avoid cluelessness about total consequences even under indeterminate beliefs, we need to appeal to intuitions about the consequences themselves — rather than epistemology or decision theory.[15] As I’ve argued, we’ll still be clueless after accounting for these descriptive intuitions. So I don’t see a normative view that justifies longtermism based on these intuitions.
- Direct intuition: “Longtermist action simply seems to have better ‘expected’ consequences than alternative .”
- A brute intuition in favor of doesn’t involve actually weighing up the total consequences, so it doesn’t carry the “stakes” of those consequences. If we instead take this intuition to be evidence about the intervention’s impact, then we’re back to option (2) above! (See “Implicit” in this post.)
So, each of these reasons is either a very shaky grounding for a normative view, or not normative at all. This suggests I shouldn’t assign an overwhelmingly large .
By contrast, to me there are rather compelling normative reasons behind indeterminate beliefs and consequentialist bracketing: It’s not that I believe, say, the bracketed-out effects of my actions on the far future precisely cancel out. Instead, I have an intuition that upon reflection, I would endorse making decisions by putting zero weight on the set of consequences I’m clueless about. (A more thorough treatment of this point is for another post.) That said, again, the theoretical hurdles to making this idea rigorous suggest I shouldn’t put much absolute weight on consequentialist bracketing.
Other potential implications to explore
Here are some other possible implications I’m less confident in than the above.
Less-clueless consequentialist views? So far, I’ve argued that metanormative bracketing can give action guidance via non-consequentialist views or consequentialist bracketing. We can also consider whether some variants of consequentialism (with or without bracketing) are less prone to cluelessness than others, and hence wouldn’t be metanormatively bracketed out. I’m skeptical that any plausible variant of impartial consequentialism, combined with maximality, avoids radical cluelessness.[16] However, we could drop either impartiality or maximality.
First, we might put some weight on consequentialist axiologies that intrinsically discount “distant” consequences, which aren’t prone to cluelessness (Vinding). See here for my reservations about this idea.
Second, what if some consequentialist axiologies are more or less action-guiding when combined with consequentialist bracketing? Take this example by Clifton:
Consider an intervention to reduce the consumption of animal products. This prevents the terrible suffering of a group of farmed animals, call them . But, perversely, it may increase expected suffering among wild animals, call them . This is because farmed animals reduce wild animal habitat, and wild animals may live net-negative lives, so that preventing their existence might be good. But we are clueless about the total effects accounting for and together (and we are clueless about the total other effects, too). So, we can construct a maximal bracket-set favoring the dietary change intervention by taking the locations of value in , or we can construct a maximal bracket-set favoring not doing the dietary change intervention by taking those in .
The “wild animals may live net-negative lives” step in this argument is highly plausible under suffering-focused consequentialism. Thus the suffering-focused view would say it’s permissible to do the intervention or not do it. But a classical utilitarian, say, arguably should be clueless about whether wild animals’ lives are bad (yet not clueless about the badness of farmed animal lives). So they’d have a unique (consequentialist) maximal bracket-set that says the intervention is required. Overall, someone who’s highly sympathetic to a suffering-focused view, yet puts some weight on classical utilitarianism, might therefore have a reason to favor the dietary change intervention.
Conditional longtermism? While I said above that I think metanormative bracketing supports neartermism, maybe the specific implications vary across decision situations. For example:
- On one hand, suppose you’re deciding what to dedicate your career to. Going with a longtermist cause area might have significant opportunity costs with respect to consequentialist bracketing. So metanormative bracketing seems to (at least) permit the neartermist option.
- On the other hand, suppose you urgently need to give strategic advice to a friend working in a safety team at an AI lab. This is a high-stakes decision with respect to longtermist views, and consequentialist bracketing wouldn’t consider it too costly to think about the advice (at least in many cases). Then, I think metanormative bracketing would require giving the advice recommended by the longtermist views you give weight to.
Acknowledgments
Thanks to Magnus Vinding, Michael St. Jules, Sandstone McNamara, Nicolas Macé, Laura Leighton, Kuutti Lappalainen, Sylvester Kollin, Alex Kastner, Clare Harris, Mal Graham, Philippa Evans, Luke Dawes, Jesse Clifton, and Jim Buhler for helpful feedback. I edited this post with assistance from Claude and ChatGPT.
Appendix: Example where metanormative bracketing is sensitive to individuation of normative views
Kuutti Lappalainen proposed the following case:
- An engineer, Elena, finds a dangerous design flaw in some product. She considers whether to leak to the press (has the best consequences, but disloyal) or report internally (loyal, but not impartially best).
- Elena has:
- 60% weight on consequentialism with slight partiality, i.e., a view that says she should mostly “do the most good”, but can give a bit more weight to those she has special commitments to;
- 40% on virtue ethics. (Call this Partition A.)
- Yet she could also think of herself as putting:
- 30% weight on purely impartial consequentialism;
- 30% on purely partial consequentialism.
- 20% on virtue ethics that gives higher priority to justice/honesty; and
- 20% on virtue ethics that gives higher priority to loyalty. (Call this Partition B.)
- Suppose Elena considers all these normative views to be intertheoretically comparable. The differences in choiceworthiness of the two options, under each of the two partitions, are in the following tables.
| Partition A | : | : |
|---|---|---|
| Partition B | : | : | : | : |
|---|---|---|---|---|
For both partitions, the interval of expected choiceworthiness over the full set of normative views is . Since this interval crosses zero, is incomparable to with respect to the full set of views.
Then, under Partition A, both and are maximal bracket-sets. Since yet , both and are permissible.
However, under partition B:
- .
- .
- .
- .
Thus, for all the maximal bracket-sets (the first three subsets in the list above) for this partition, . And so only is permissible.
References
Elkin, Lee. 2024. “Normative Uncertainty Meets Voting Theory.” Synthese 203 (6). https://doi.org/10.1007/s11229-024-04644-6.
Greaves, Hilary. 2016. “Cluelessness.” Proceedings of the Aristotelian Society 116 (3): 311–39.
Hedden, Brian. 2024. “Parity and Pareto.” Philosophy and Phenomenological Research 109 (2): 575–92.
Hedden, Brian, and Daniel Muñoz. 2024. “Dimensions of Value.” Noûs (Detroit, Mich.) 58 (2): 291–305.
Kollin, Sylvester, Jesse Clifton, Anthony DiGiovanni, and Nicolas Macé. 2025. “Bracketing Cluelessness.” Working paper. https://longtermrisk.org/files/Bracketing_Cluelessness.pdf.
MacAskill, William. 2013. “The Infectiousness of Nihilism.” Ethics 123 (3): 508–20.
———. 2016. “Normative Uncertainty as a Voting Problem.” Mind; a Quarterly Review of Psychology and Philosophy 125 (500): 967–1004.
MacAskill, William, Krister Bykvist, and Toby Ord. 2020. Moral Uncertainty. London, England: Oxford University Press.
MacAskill, William and Toby Ord. 2018. “Why Maximize Expected Choice-Worthiness?” Noûs 54(2): 327-353.
Mogensen, Andreas L. 2020. “Maximal Cluelessness.” The Philosophical Quarterly 71 (1): 141–62.
Tarsney, Christian J. 2021. “Vive La Différence? Structural Diversity as a Challenge for Metanormative Theories.” Ethics 131 (2): 151–82.
Yim, Lok Lam. 2019. “The Cluelessness Objection Revisited.” Proceedings of the Aristotelian Society 119 (3): 321–24.
- ^
Greaves (2016) argues that cases that seem similar to “kick the puppy?” are only instances of simple cluelessness. Following Yim (2019) and MichaelA, however, I think it’s far more plausible that we have complex cluelessness in these cases.
- ^
I usually prefer to say “impartial altruism” here, because non-purely-consequentialist moral theories can still be vulnerable to radical cluelessness, if they give sufficiently high weight to consequences when ranking actions’ choiceworthiness (i.e., they’re vulnerable insofar as they’re consequentialist). But I’ll use “consequentialism” here, because this post will analyze pluralistic normative views, and it will be helpful to think of non-purely-consequentialist moral theories as pluralistically giving weight to both consequentialism and non-consequentialism.
- ^
See his “Argument 1”.
- ^
I’ll specifically consider “top-down bracketing” (Kollin et al. 2025, Sec. 5.2).
- ^
We might also try formulating bracketing in a different way entirely: Instead of saying “we’re clueless about these individual consequences, so we should bracket them out”, there may be qualitative differences between sets of consequences, such that we could bracket out some sets. Clifton gives a brief sketch of one version of this. But this idea hasn’t been made precise yet.
- ^
Notes:
- Since multiple normative views might entail different sets of distributions , in general we’d need to iterate over all these sets. But for simplicity I’ll just consider one set .
- You can think of this rule as, roughly, applying maximality to aggregated choiceworthiness over the set of normative views, rather than aggregated value.
- ^
To be precise, MacAskill et al.’s proposal is: Take the set of “coherent completions” of the view that posits incomparability, i.e., assignments of choiceworthiness to the available actions that have the same ordering as whenever has an ordering for a given pair of actions. Then variance-normalize each view and each coherent completion, and rule out any actions with lower normalized expected choiceworthiness than some alternative for the whole set of coherent completions. I’ve set up the example in Table 1 below to already be variance-normalized. And the example applies just as well to the coherent completions approach as to the imprecise generalization of MEC. So the problem of high weight on a clueless view applies to MacAskill et al.’s proposal overall.
- ^
Of course, for the same reason we endorse indeterminate beliefs about empirical hypotheses, i.e., avoiding arbitrary precision, we might also endorse indeterminate weights on normative views.
- ^
I’ve omitted and from the notation here for readability, since we’ll consider a fixed and throughout the whole model.
- ^
Cf. Hedden (2024), and Kollin et al.’s (2025, Sec. 4) response in the context of consequentialist bracketing.
- ^
We might try extending this method to handle, e.g., cases where doesn’t give us a cardinal margin of victory for some pair of actions. While it’s not obvious how to do so, dealing with a mix of cardinal and purely ordinal views is a general problem for metanormative theories (Tarsney 2021). So for our purposes, it’s enough to be assured that metanormative bracketing handles unambiguous cases like MacAskill’s.
- ^
H/t Jesse Clifton for emphasizing to me the importance of this point.
- ^
While I’ve touched on similar themes previously, this section is meant to make the argument more carefully and expand on it.
- ^
For example, I don’t think there’s a sensible way to cash out the intuition that precise beliefs “contain more information”.
- ^
Clifton proposes a decision rule for imprecise probabilities that could in principle justify longtermist interventions. In practice, as Clifton says himself, I think reasonable beliefs about far-future consequences will be so vague that this decision rule isn’t applicable. (Non-vague imprecise probabilities / EVs, meanwhile, have the same problems as we saw in option (1) in the main text.)
- ^
E.g., both classical and suffering-focused utilitarians seem to be clueless due to their unawareness of many important possibilities.

Say I find ex post neartermism (Vasco's view that our impact washes out, ex post, after say 100 years) more plausible than consequentialist bracketing being both correct and action-guiding.
My favorite normative view (impartial consequentialism + plausible epistemic principles + maximality) gives me two options. Either:
Would you say that what dictates my view on (a)vs(b) is my uncertainty between different epistemic principles, such that I can dichotomize my favorite normative view based on the epistemic drivers of (a)vs(b)? (Such that, then, MNB allows me to bracket out the new normative view that implies (a) and bracket in the new normative view that implies (b), assuming no sensitivity to individuation.)
If not, I find it a bit arbitrary that MNB allows your "bracket in consequentialist bracketing" move and not this "bracket in ex post neartermism" move.
It seems pretty implausible to me that there are distinct normative principles that, combined with the principle of non-arbitrariness I mention in the "Problem 1" section, imply (b). Instead I suspect Vasco is reasoning about the implications of epistemic principles (applied to our evidence) in a way I'd find uncompelling even if I endorsed precise Bayesianism. So I think I'd answer "no" to your question. But I don't understand Vasco's view well enough to be confident.
Can you explain more why answering "no" makes metanormatively bracketing in consequentialist bracketing (a bit) arbitrary? My thinking is: Let E be epistemic principles that, among other things, require non-arbitrariness. (So, normative views that involve E might provide strong reasons for choice, all else equal.) If it's sufficiently implausible that E would imply Vasco's view, then E will still leave us clueless, because of insensitivity to mild sweetening.
Oh so for the sake of argument, assume the implications he sees are compelling. You are unsure about whether your good epistemic principles E imply (a) or (b).[1]
So then, the difference between (a) and (b) is purely empirical, and MNB does not allow me to compare (a) and (b), right? This is what I'd find a bit arbitrary, at first glance. The isolated fact that the difference between (a) and (b) is technically empirical and not normative doesn't feel like a good reason to say that your "bracket in consequentialist bracketing" move is ok but not the "bracket in ex post neartermism" move (with my generous assumptions in favor of ex post neartermism).
I don't mean to argue that this is a reasonable assumption. It's just a useful one for me to understand what moves MNB does and does not allow. If you find this assumption hard to make, imagine that you learn that we likely are in simulation that is gonna shut down in 100 years and that the simulators aren't watching us (so we don't impact them).
Gotcha, thanks! Yeah, I think it's fair to be somewhat suspicious of giving special status to "normative views". I'm still sympathetic to doing so for the reasons I mention in the post (here). But it would be great to dig into this more.